Fourier Analysis

Introduction

Purpose

This article is intended to introduce Fourier analysis as a tool for the frequency analysis of time-series data. There is some background provided on Fourier Series and on the different types of Fourier transform, this is aimed at giving the reader a clearer idea of how Fourier analysis works, but will include no mathematical derivations. After that, the focus of this article will be on applying the Discrete Fourier Transform (DFT), and on an extension to this method known as the Multitaper method. All visualisations and accompanying scripts are freely available in the Github repository.

Fourier Analysis

Fourier analysis is a field of mathematics concerned with understanding how arbitrary functions can be represented as a superposition of simple periodic functions. Modern Fourier analysis is an extension of the concept of Fourier series; if a general function can be approximated by a combination of regular periodic functions then studying these component functions can reveal properties of the original function. In this way, a Fourier transform can convert time-series data into the frequency domain and then provide information on the amplitude and phase of these underlying frequencies.

Background

Fourier Series

A Fourier series F(x) is the representation of an arbitrary periodic function f(x) as a sum of trigonometric functions. The trigonometric functions most commonly used to construct the sum are the Sine and Cosine functions, this is called the sine-cosine form of the Fourier series (Equation 1.1). The sum is calculated using the coefficients a₀, a_n and a_b (Equations 1.2 - 1.4) over an analysis period P = P₁ - P₂.

Equation 1.1

Equation 1.2

Equation 1.3

Equation 1.4

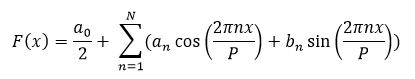
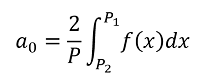
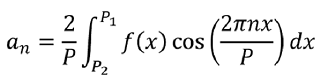
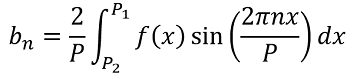
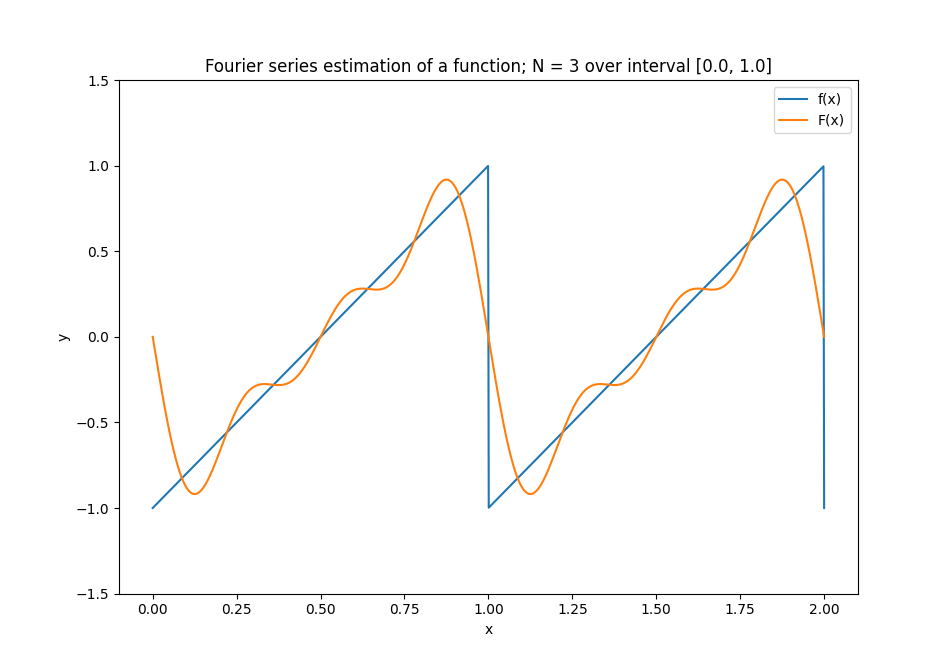
Figure 1 demonstrates the approximation of a sawtooth function by a Fourier series, the two functions typically become equal as N is increased towards infinity.

Figure 1

Euler’s formula (Equation 1.5) can be used to rewrite the sine-cosine form of the Fourier series in the exponential form (Equation 1.6) with the new Fourier coefficient c_n (Equation 1.7). This form of the Fourier series is used because it is allows for the input function f(x) to be complex, it is therefore commonly used for representing Fourier transforms, which will be introduced in the next section.

Equation 1.5

Equation 1.6

Equation 1.7

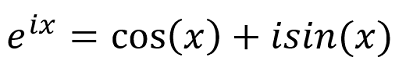
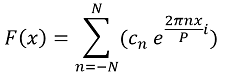
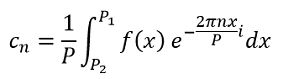
Fourier series allow arbitrary periodic functions to be rewritten in a simpler way, but real world signals are often non-periodic and so can not be represented using Equation 1.6. Fourier transforms allow us to extend these concepts to non-periodic functions

Fourier transforms

This section will briefly introduce and distinguish between three types of Fourier transform: the Continuous Fourier Transform (CFT), the Discrete-time Fourier Transform (DTFT) and the Discrete Fourier Transform (DFT). These transforms all have slightly different purposes, once these are identified it will be clear why the DFT is chosen to apply to time-series data.